 informatematica
informatematica


|
16/03/2011
classe terza
equiestensione di parallelogrammi
funzioni a incrementi additivi
trasformazioni geometriche su grafici di funzioni 14/02/2011 PUG (Parametrical URL Graphics: PGC usata da URL) download - mini-download - esempi - facebook 26/01/2011 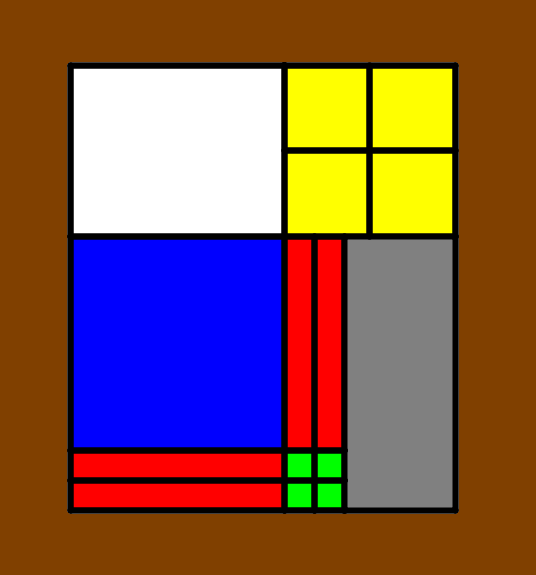 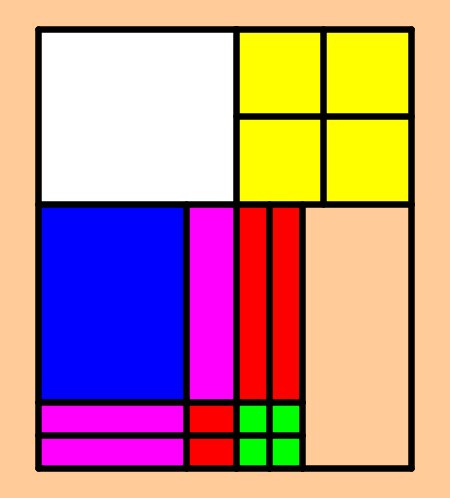 Una dimostrazione del teorema di Pitagora Questa mia dimostrazione utilizza il secondo teorema di Euclide , che ben si presta ad un approccio geometrico-analitico al teorema di Pitagora, in quanto concerne lunghezze di segmenti coordinati (ossia paralleli agli assi cartesiani) e "valuta" la misura del segmento non coordinato (l'ipotenusa c) tramite una riflessione (simmetria assiale). Altre classiche dimostrazioni utilizzavano, invece, il primo teorema di Euclide, la cui dimostrazione puramente analitica richiedeva (circolarmente) il teorema di Pitagora stesso, dal momento che coinvolge segmenti non coordinati con gli assi. L'applet dinamica realizzata con GeoGebra è in:http://w3.romascuola.net/gspes/geogebra/pitagora2.html (costruita con animazione con PGC-PUG è qui; muovi in orizzontale il punto c) Un'altra bella applet a riguardo, con illustrazione in inglese, è in: http://www.cut-the-knot.org/Curriculum/Geometry/SperanzaPyth.shtml e il relazionamento diretto del secondo teorema di Euclide al concetto di "modulo" è illustrato in: http://w3.romascuola.net/gspes/geogebra/pitagora-euclide.html
Il confronto tra le due costruzioni relative ai due teoremi di Euclide è in: 18/01/2011 funzioni lineari: rette nel piano cartesiano funzioni quadratiche: parabole nel piano cartesiano trasformazioni geometriche su funzioni trasformazione di un numero periodico in frazione introduzione al concetto di derivata
Due dimostrazioni del teorema di Pitagora 14/10/2010 operazioni e operazioni grafiche animazione sulla genesi del piano cartesiano alberi sintattici degli assiomi algebrici elementari esercizi sulle equazioni di primo grado testo introduttivo di matematica programmazione didattica per l'A.S. 2010-2011 22/09/2010 Indice per argomenti di "Informatematica" Matematica per le superiori (Wikibooks) Sito di "ripasso di matematica" (ripmat.it) PUG (Parametric URL Graphics: PGC usata da URL) Scarica PGC (Plane Graphic Calculator) 30/06/2010 Asis Onlus - IX Corso nazionale residenziale Del "più" e del "per" (relazione tenuta al IX corso ASIS) 11/05/2010
Teorema fondamentale del calcolo 17/04/2010
Funzioni, simmetrie dei loro grafici e trasformazioni geometriche su di essi:
http://precorso.dicom.uninsubria.it/lezioni/funzioni.htm
http://www.batmath.it/matematica/a_grafelem/grafelem.htm http://macosa.dima.unige.it/om/voci/funz2/funz2.htm#5 http://newrobin.mat.unimi.it/users/mantovani/Arg01/Teoria1B.pdf ( http://newrobin.mat.unimi.it/users/mantovani/Contenuticorso.html ) http://www.mimmocorrado.it/mat/ana/studiofunzione/graficideducibili.pdf http://it.wikibooks.org/wiki/Matematica_per_le_superiori/Studio_grafico_delle_funzioni 15/03/2010
Schema riassuntivo sulle funzioni logaritmiche ( v. anche log )
Sistemi di riferimento cartesiani piani e operazioni elementari sui numeri reali 04/03/2010
26/02/2010
Un'applicazione del numero di Nepero in meccanica ( v. anche e )
16/02/2010
10/12/2009 17/11/2009
14/10/2009
teoremi del calcolo algebrico elementare
mappe sul calcolo algebrico elementare retta e proporzionalità diretta
insiemi numerici 08/10/2009 (clicca sulla figura e tieni premuta la barra spaziatrice) 25/09/2009 24/09/2009
strutture numeriche (e non)
operazioni (v. anche C ) operazioni grafiche 21/09/2009 approssimazione polinomiale della funzione exp 18/09/2009 21/06/2009 10/06/2009 02/05/2009 tutorial di GeoGebra
miniguida di GeoGebra elaborazioni grafiche con GeoGebra versioni di GeoGebra learn and use GeoGebra 20/03/2009 regole di catena 06/03/2009 24/02/2009 Premi ripetutamente il pulsante Step oppure la barra spaziatrice Muovi in orizzontale il punto cursore c verso destra o verso sinistra Approssimazione tramite riga (ovvero tramite parallelismo) Viene generata la funzione esponenziale passante per il punto (h,k), con k=1+h. 17/02/2009 12/02/2009
13/11/2008 derivazione e plurirettangoli (teorema fondamentale del calcolo) La funzione in blu è l'approssimazione della funzione seno fra a e b con una poligonale ottenuta congiungendo punti del grafico della funzione seno scelti con ascisse che si susseguono a intervalli uguali, di ampiezza diciamo Δx, fra a e b. Aumentando l'ascissa del punto d aumenta la densità di tale insieme di punti. Muovendo fra ascissa 0 e ascissa 1 il punto di controllo c, si muove il vertice mobile m sulla suddetta poligonale e viene disegnato il triangolo verde che caratterizza la salita dal vertice m al vertice successivo, quindi si espande tale triangolo verde in un triangolo simile, in colore viola, avente cateto orizzontale unitario, che riporta la pendenza di tale salita (da m al vertice successivo) come ordinata corrispondente all'ascissa di m sul grafico "a scala" rosso. Pertanto la funzione rossa a scala rappresenta il grafico delle pendenze della poligonale relative agli intervallini di base Δx. La funzione a scala crea dei rettangoli ognuno dei quali ha area pari alla base Δx moltiplicata per l'altezza misurata sul grafico rosso (che può essere positiva o negativa), ovvero moltiplicata per la pendenza della salita a partire da m; pertanto tale area rappresenta esattamente la salita nel triangolino verde (nota che l'area è positiva se la salita è positiva ed è negativa se la salita è negativa). Si verifica perciò che la somma delle salite lungo i triangoli verdi, pari in totale alla differenza sin b - sin a (tale salita nella posizione iniziale di a e b in figura è nulla, ma puoi modificare col mouse sia a sia b), coincide con la somma delle aree dei rettangoli aventi i lati rossi. Facendo tendere a infinito il numero dei punti di suddivisione, la funzione rossa tende a diventare la derivata della funzione blu, e si verifica così graficamente che la differenza sin b - sin a è pari all'area compresa fra la derivata della funzione seno (che è il coseno) e l'asse delle ascisse (valutata a partire aall'ascissa a fino ad arrivare all'ascissa b (area che viene chiamata "integrale indefinito della funzione coseno esteso da a a b").
29/10/2008 la derivazione grafica di una funzione
17/06/2008 01/02/2008 la circonferenza goniometrica (classe quarta)
|
dankon al squidfingers pro la paĝfonoj