Del "più" e del "per": dal "far di conto" al "vedere in calcolo" ;
l'introduzione combinata di algebra e geometria

(ovvero: come la dinamizzazione computerizzata del disegno consente l'introduzione combinata dei concetti elementari dell'algebra e della geometria)

Gaetano Speranza
relazione al IX Corso ASIS
(Associazione Stampa Italiana Scolastica)
luglio 2010


Introduzione

Annose sono le multiformi riflessioni didattiche legate alla diffusa percezione (non limitata ai soli studenti) dei concetti matematici come alternanza di "mero conto numerico" e di "astrusità astratta di calcolo elaborativo", percezione pregiudiziale in larga parte dovuta alle stesse modalità di insegnamento mnemonico-precettistiche in cui la tradizione scolastica ha sclerotizzato la trasmissione di tale materia, modalità che rischiano fortemente di permanere, o di essere ripercorse in nuove vesti, in una visione comportamentistica, addestramentale, e in fin dei conti vanamente utilitaristica, della trasmissione per "moduli-oggetto" (ossia legati alle specifiche competenze acquisite, alle singole "performance" topiche) anziché secondo "moduli-processo" (ovvero legati alle fasi olistiche della comprensione, e quindi dell'apprendimento, alla "máthesis").
Gli acuti, e per certi versi necessariamente provocatorî, punti di vista esposti, ad esempio, da Lucio Russo in "Segmenti e bastoncini" e da Paul Lockhart in "Contro l'ora di matematica" enucleano magistralmente la problematica dello "avvilimento della cultura" tramite lo "svilimento della formula".
Molti tra i nodi basilari di tali riflessioni che hanno persistito al vaglio del tempo e della percorribilità curricolare effettiva puntano alla posizione didattico-epistemologica secondo cui la comprensione del linguaggio base della matematica, ossia il formalismo algebrico, non trae beneficio, al livello necessariamente elementare dell'itinerario scolastico, da una trattazione contenutisticamente più generale e fondazionale (come quella insiemistica), pur essa veicolata dallo stesso formalismo algebrico, bensì richiede un lavoro di esplicitazione e analisi esemplificativa, come pure di sintesi rappresentazionale, del parallelismo tra la formulazione simbolica e alcune macrostrutture linguistiche della lingua naturale del discente, nonché una implementazione di tale formalizzazione in un modello concreto, quale è quello grafico del piano.
Si presenta in questa esposizione, pertanto, una modalità di introduzione dei concetti numerici e operazionali che può fortemente far leva sull'utilizzo di un software di geometria dinamica combinato con un software di mappatura gerarchica. Il software di geometria dinamica è utilizzato per la visualizzazione degli oggetti e dei processi del modello grafico, nella mutevolezza delle loro possibili interrelazioni, e potrebbe essere, ad esempio, GeoGebra o Cabri-Géomètre, per una tipologia di input di tipo duplice algebrico e geometrico, coadiuvato, a un livello di maggiore maturità e competenza formale, da PGC (“Plane Graphic Calculator”, ovvero “Calcolatrice Grafica Piana”, che è un'Applet Java utilizzabile mediante browser) per una tipologia di input puramente algebrico.
D'altro canto un software di mappatura gerarchica (come ad esempio Mind Manager Smart) risulta utile per visualizzare in maniera ordinata l'analisi sintattica, ovvero "organigrammica", delle formule.
In quest'ottica la matematica elementare diventa la scienza non dei numeri bensì delle operazioni, non del risultato bensì del processo, non tanto delle somme e dei prodotti formali, quanto dell'addizionare e del moltiplicare, visti nel loro significato - eidologico ma soprattutto archetipico - di traslare e di proporzionare, "afferrando" (e verrebbe spontaneo dire "prendendo a sé", "ad-prendendo") l'intima natura di tali processi nelle relazioni simboliche cristallizzate in formula, in simil guisa di come una distribuzione di forma e colore o una stringa armonica di suoni sustanzia in oggetto d'arte l'altrimenti inafferrabile tratto dell'anima del soggetto creatore.



L'introduzione dei numeri con un approccio geometrico:
i punti salienti della teoria relativa alla struttura (C,0,+,1,R+,·,i)

Si tratta di una impostazione assiomatica delle basi della teoria elementare degli insiemi numerici che introduce assiomaticamente - sulla base di un modello grafico costruibile a partire dai soli concetti intuitivi di retta, intersezione di rette e perpendicolarità - il campo dei numeri complessi C vedendo il campo dei numeri reali R come parte "a par condicio" con il suo complemento a C.
Tale processo è di tipo "immersivo", ossia che, invece di partire dai numeri reali per costruire (ampliando R) i numeri complessi (quindi facendo “emergere” C da R, il che comporta ovviamente una previa introduzione di R stesso), parte da uno “spazio” C (che empiricamente, ossia nel modello grafico della teoria, è un piano) in cui si introducono gradualmente e incrementalmente varie strutturazioni, ritrovando “immersi” in C i vari enti che di volta in volta entrano nella scena degli oggetti costitutivi della teoria.

La prima fase di strutturazione è rappresentata dalla struttura additiva di gruppo fornita a C da un'operazione di addizione e dal suo elemento neutro 0 individuato come “origine” o “centro” in C.
Tale “piano puntato", ossia un piano con un punto privilegiato 0, permette di associare ad ogni punto P del piano stesso il “raggio vettore” partente dall'origine e terminante in P, visualizzato come freccia da 0 a P e definibile come coppia ordinata (0,P).
Ciò consente un'introduzione ai vettori, pur se, a questo livello, ancora senza nozioni moltiplicative. La regola grafica soggiacente all'operazione simbolica di addizione è quella nota del parallelogramma o della traslazione).

Gli assiomi introdotti a questo livello sono i quattro assiomi di associatività, commutatività, neutralità dello zero, simmetrizzabilità tramite opposti. Si perviene così alla parte della struttura relativa alla terna (C,0,+) e all'introduzione dell'operatore “unario” (ossia a un solo ingresso) di opposizione, il “ – “, definendo poi la sottrazione come “somma con l'opposto”. Si possono già in questo ambiente provare alcuni risultati interessanti, ad esempio:

a + b = c   se e solo se   a = c - b
- 0 = 0
- ( - a ) = a
- ( a + b ) = - a - b
- ( a - b ) = - a + b .

Di non poca istruttività è l'osservare come graficamente la somma di due punti, realizzata tramite parallelogramma, scompare quando i due punti vengono ad essere allineati con l'origine. Questo fatto presenta a un livello molto elementare la pregnanza pratica del concetto di limite, in quanto graficamente il punto somma, in questo caso, può essere approssimato quanto si vuole tramite somme di punti non allineati con l'origine. Così come è anche molto significativo il processo di estrapolazione, tipico del procedere scientifico, che conduce a mantenere valida la considerazione degli assiomi come verità sussistenti anche per i casi “limite” in cui l'esperienza grafica non conduce alla rappresentazione “esatta” degli oggetti coinvolti; estrapolazione che ripaga al momento in cui, utilizzando gli assiomi stessi nella loro portata generale, si riesce ad “acchiappare” graficamente i punti prima definibili solo come limiti mediante una costruzione grafica che fa leva sugli assiomi stessi.

Si aggiunge poi una struttura moltiplicativa, osservando che l'iterazione dell'addizione su uno stesso elemento a (a, a+a, a+a+a, …) e su uno stesso elemento b (b, b+b, b+b+b, …) porta graficamente ad avere che la retta congiungente a e b, quella congiungente a+a e b+b, quella congiungente a+a+a e b+b+b sono graficamente parallele, e quindi se si sceglie un secondo punto “privilegiato”, 1, e si danno i nomi ai punti ottenuti dalla somma iterata di 1, ovvero 2, 3, 4, … , si possono ottenere a+a, a+a+a, … tramite un processo, quello che porta alla regola grafica poi formalizzata nell'operazione di moltiplicazione, che è quello, Taletiano, di tracciare la retta(1,a) e poi condurre per un numero reale x, ossia un elemento della retta(0,1), la parallela a tale retta, ritrovando x·a come intersezione di tale ultima retta con la retta(0,a). In particolare si ritrovano 2·a, 3·a, ecc… , potendo però adesso trattare graficamente anche un generico x·a, con x reale.
Questo conduce alla struttura, arricchita rispetta a quella precedente e formalizzata come (C,0,+,1,R+,·), in cui R=retta(0,1) corrisponde all'unione della semiretta positiva (il “verso positivo” del piano cartesiano tradizionale), che è il nuovo ente primitivo che ritroviamo “immerso” (nel senso di “contenuto”) in C, della sua opposta, la semiretta negativa che nasce dal raccogliere tutti gli opposti dei punti della semiretta positiva, e dell'origine.
Quindi R = R+ U (-R+) U {0}.
L'operazione di moltiplicazione è qui un'operazione definita su RxC e a valori in C, che porta (x,a) nel multiplo x·a ed è realizzata graficamente tramite la costruzione taletiana, mediante rette e parallelismo, dei triangoli “proporzionali” (0,1,a) e (0,x,x·a). Questo diventa il primo esempio pregnante di “similitudine” tra due figure.
Gli assiomi, da verificare graficamente, sono, anche qui, quattro: la associatività [ (xy)a=x(ya) ], la commutatività ( xy=yx ), la neutralità dell'uno ( 1a=a ), e la invertibilità della funzione b -> xb, ottenuta fissando un x reale e non nullo, per cui dato a, esiste uno ed un solo b tale che xb=a (ciò porta a invertire le precedente regola di Talete, partendo dal congiungere x con a (e non 1 con a, come per la moltiplicazione) per poi determinare la parallela passante per 1 e determinando come intersezione con la retta(0,a) il punto b=a/x.
Su una figura esplorabile dinamicamente è possibile far vedere come, avvicinando x allo 0 sull'asse R, in corrispondenza a/x si allontana sempre di più “verso infinito” sull'asse Ra.
In effetti la commutatività e la invertibilità sarebbero deducibili dalle ipotesi che succesivamente verranno fatte per caratterizzare “topologicamente” R come insieme ordinato continuo, ma per la loro pregnanza grafica (nonché per la difficoltà della loro deduzione dalla struttura topologica di R) è consigliabile introdurle come assiomi ulteriori.

Inoltre due assiomi, sempre da verificare graficamente, interrelazionano le operazioni di addizione e di moltiplicazione; si tratta delle due proprietà distributive:
a sinistra: x·(a+b) = x·a + x·b (distributività del moltiplicatore)
a destra: (x+y)·a = x·a + y·a (distributività del moltiplicando),
notando come, nonostante la loro analogia formale, esse portino a due rappresentazioni grafiche notevolmente diverse.
La distributività della moltiplicazione rispetto all'addizione è il “cuore” semantico della moltiplicazione stessa, in quanto comporta che la moltiplicazione agisce come reiterazione dell'addizione ( ad esempio: 3a=(1+1+1)a=a+a+a ) e che un prodotto xy è “direttamente proporzionale” a ognuno dei suoi fattori ( ad esempio: (2x)y=(x+x)y=xy+xy=2(xy) ).

Successivamente si arricchisce la struttura di un punto i (unità immaginaria, in contrapposizione all'unità reale 1) non appartenente ad R, per costruire la retta I=Ri (asse immaginario). Il modello empirico-grafico che si prende a semantica della teoria è quello ortonormale e si formalizzano così i concetti di "verso" (semivarietà lineare), “verso di rotazione antiorario o orario”, e, introducendo opportuni assiomi di ordinamento in R (oppure sulla semiretta R+), quelli di "densità", di "continuità" (assenza di "buchi"). La dimensionalità (esistenza di due versi indipendenti), è semplicemente asserita dall'indipendenza di i da 1, nonché dal fatto che la coppia (1,i) genera tutto C, delegando alla terna (0,1,i) i criteri empirici di “ortogonalità” e di “equidistanza”.

C'è da precisare che mentre nelle usuali trattazioni degli insiemi numerici è il numero ad esser posto a fondamento di modelli analitici di teorie sintetiche (la cosiddetta "geometria analitica", che poggia sulla geometria sintetica Euclidea), qui una teoria di tipo sintetico-vettoriale (o meglio, di "spazio vettoriale su un campo di scalari costituito da un proprio sottospazio unidimensionale e continuo") è alla base dell'introduzione stessa dei numeri, quindi si porrebbe essa stessa a modello geometrico di una eventuale preesistente teoria costruttiva dei numeri, così come si fa quando si introducono i monoidi di grandezze).

Introducendo le combinazioni lineari x+yi, che costituiscono il piano C=R+Ri=R+I, nascono le isometrie scaturenti dal cambiare il segno o scambiare le coordinate, ad esempio la coniugazione conj( x+yi):=x-yi e l'ortogonalità (o meglio “ortonormalità”) ort(x+yi):=-y+xi, trasformazioni facilmente interpretabili e giustificabili dal punto di vista grafico.
Le composizioni di tali due isometrie di base conducono a otto isometrie fondamentali, quattro delle quali sono simmetrie assiali - rispetto agli assi R e I e rispetto alle due bisettrici di tali assi, che sono R(1+i) e R(1-i) – le altre quattro essendo, invece, rotazioni – quelle di 0, 1, 2, 3 quadranti, ovvero l'identità, la rotazione di un angolo retto in senso antiorario, l'opposizione e la rotazione di un angolo retto in senso orario.
Queste otto simmetrie fondamentali, che tengono fissa l'origine o una intera retta passante per l'origine, consentono di svolgere delle sperimentazioni “caleidoscopiche”, mostrando come una qualunque configurazione, unita alle sue sette isometriche che scaturiscono da quelle di queste isometrie che non sono banali (ossia che non sono l'identità), viene a formare una figura armoniosa del tipo di un “mandala”.

Un'osservazione teorica è d'obbligo: dire che ort costruisce "l'ortogonale isometrico (ossia ortonormale) antiorario" non è meno convenzionale che dire che due vettori u e v sono ortogonali e congruenti rispetto ad un prodotto scalare fra gli infiniti possibili che possono essere introdotti nel piano, equivalenti a meno di trasformazioni lineari non degeneri.
Si può anche rilevare come la costruzione dell'ortonormale antiorario eseguita in questo modo ricalchi la maniera secondo cui istintivamente ricostruiamo il riconoscimento della perpendicolarità riferendoci ad una coppia di base costituita sostanzialmente dall'orizzontale del terreno e dalla nostra posizione verticale rispetto ad esso (oppure, per fare un'altra analogia, ortogonalizzando la diagonale di un rettangolo ruotando tutto il rettangolo, così come si ruota un quadro).

Partendo dalla rotazione di un angolo retto antioraria – quella che associa ad 1 il punto i – rotazione che indicheremo con il simbolo operatoriale ort, resta facile ora estendere la moltiplicazione a coefficiente reale ad una operazione di moltiplicazione definita su tutti i fattori che il piano fornisce, ossia definita su CxC. Il criterio è sempre quello della similitudine fra i triangoli (0,1,a) e (0,x,x·a), solo che adesso ad x si sostituisce un generico punto del piano z, per cui i triangoli “proporzionali” diventano (0,1,a) e (0,z,z·a). Il terzo vertice z·a del secondo triangolo è facilemte determinabile in base all'osservazione che esso deve avere, rispetto alla coppia di riferimento (z, ort(z)) le stesse coordinate che ha il punto a riapetto alla coppia di riferimento (1,i), per cui si ha z·a = ax z + ay ort(z).
Svolgendo tale espressione in termini anche delle coordinate di z vien fuori che tale moltiplicazione è commutativa e che quindi, indicando con x e y le componenti di z (ossia z=x+yi) si ha anche z·a = x a + y ort(a), il che permette di osservare che moltiplicare z per a significa determinare un punto che ha rispetto ad a (e al suo ortogonale) le componenti che z ha rispetto ad 1 (e al suo ortogonale i). Questo fatto riconduce all'idea “archetipica” di moltiplicazione come ad una “proporzionalizzazione” dal riferirsi all'unità al riferirsi ad un altro oggetto differente dall'unità che prenda le veci di “nuovo riferimento”. Del resto anche nel caso della moltiplicazione elementare il 3 “per” 2, ossia il “tre volte due” non è altro che ciò che si ricava da 3=1+1+1 sostituendo ad ogni 1 un 2, per avere 3·2=2+2+2, quindi è quel numero che è “costituito” dal 2 così come il 3 è costituito da 1, e pertanto diventa un 3 costruito “per mezzo” di 2.

La trasformzione che associa ad ogni z il punto z·a ottenuto esprimendo rispetto ad a le componenti di z è detta “roto-omotetia”; “omo-tetia” perché z si “pone” (in greco tìthemi) rispetto a 1 così come z·a si pone rispetto ad a; e “roto-” in quanto il fatto che a non sia necessariamente un numero reale (quindi non necessariamente sull'asse dell'uno) comporta nella posizione di z e di z·a un'angolatura rispetto all'asse reale e all'asse Rz congiungente 0 e z, angolatura che è la stessa passando da R a Ra e da Rz a R(z·a).

A questo punto, dal piano e dalla moltiplicazione in C, introdotta come cambiamento di sistema di riferimento e alla base delle roto-omotetie (e in particolare delle omotetie e delle rotazioni), si possono far scaturire le problematiche di tipo isometrico, pitagorico, metrico e numerico-irrazionale; ad esempio le seguenti:
- una roto-omotetia   z → z·a   è detta rotazione quando, così come porta 1 in a, porta il coniugato di a in 1, ossia se  conj(a)·a=1; in tal caso il punto   a   è detto "unitario" e l'insieme dei numeri unitari è detto "circonferenza goniometrica" ;
- l'uguaglianza   conj(a)·a=1   esprime il teorema di Pitagora per i punti unitari, in quanto significa:   ax2 + ay2 = 1 ;
- ogni punto   a   non nullo ha un “versore” unitario ( indicato come vers(a) ), che è il punto unitario che sta sulla semiretta R+·a (ossia l'insieme dei multipli di a con coefficienti reali positivi) ;
- il fattore positivo   k   tale che   k·vers(a)=a   è quel che vien detto il “modulo” di a ( indicato come |a| ), ed è il numero reale che esprime la distanza di a da 0, ovvero il vettore   a   “misurato tramite” il suo versore ;
- la distanza fra due punti   z   e   w   è il modulo   |z-w| ;
- il modulo   |1+i|   è la "famigerata" radice di 2, che è il primo esempio che solitamente si presenta di "numero irrazionale" .

* * *

Tale sviluppo della teoria - ulteriore passo verso la “semplificazione assiomatico-intuitiva” nella catena di assiomatizzazioni della geometria elementare che passa, per citare gli esempi più noti, per i nodi legati ai nomi di Dieudonné, Choquet e Papy - pare pertanto essere un modo per:

a1) evitare di introdurre l'ampliamento di R a C come una "uscita cervellotica" e puramente algebrica (per cui i viene ad essere una radice quadrata "strana" di -1);

a2) evitare di creare (in barba ai monomorfismi immersivi) nei neuroni degli studenti una disparità di trattamento fra R e C, per cui R stesso è diverso se visto da solo o come asse reale;

b1) usare subito nozioni geometriche intuitive ma subito formalizzate lavorando nel contempo su numeri in modo grafico ( ad esempio con un software di geometria dinamica ), fra l'altro permettendo di esplicitare i ruoli di sintassi e semantica, teoria formale e interpretazione;

b2) viceversa rispetto al punto (b), interpretare ogni volta geometricamente il frutto di calcolo algebrico (senza delegare tutto alla geometria analitica procrastinata, magari al triennio);

c) trovare subito un'esemplificazione semplice, e a livello intuitivo ed elementare, del concetto di “limite” nell'addizionare punti allineati con l'origine (scompaiono i parallelogrammi) o nel moltiplicare un numero reale per un altro numero reale (scompaiono i triangoli simili);

d1) “dare” all'addizione “ciò che è dello zero” e alla moltiplicazione “ciò che è dell'uno”.

d2) associare addizione e traslazioni da una parte e moltiplicazione e roto-omotetie (in particolare le omotetie e le rotazioni) dall'altra, facendo assumere a rette e circonferenze ruolo di figura fondamentale per i due tipi di isometria, magari con riflessioni sul concetto di curvatura e di punto all'infinito;

d3) vedere 0 come il punto a "potenziale additivo nullo" (origine del piano) e 1 come quello a "potenziale moltiplicativo nullo" (origine degli angoli, definiti come rotazioni intorno a 0), polarizzando la struttura di C in vettori (frecce "dritte") da una parte e "rotatori" (numeri complessi unitari, alias frecce "arcuate") dall'altra;

d4) vedere la moltiplicazione come operazione introdotta gradualmente sulla base dell'addizione (proporzionalità diretta naturale e frazionaria) e poi della continuità e dell'ortogonalità (e non come operazione asetticamente distributiva come si fa nella usuale introduzione assiomatica di R); e inoltre non degradare al rango di "moltiplicazione di binomi" la moltiplicazione in C;

e1) svincolare il concetto di distanza da un'ambigua e non integrata oscillazione fra nozioni di geometria “sintetica” (sempre più raramente formalizzate a livello scolastico) e norma pitagorica su numeri o coppie numeriche;

e2) preparare "eulerianamente" la strada alla misura in radianti (altro punto di glissement nelle trattazioni elementari della goniometria) e alle funzioni goniometriche tramite la visualizzazione della spirale (1+i/n)k con k=0,...,n ed n intero positivo e sempre più grande; lo stesso con la "archificazione" di t e (1+it/n)k con k=0,...,n (per cui exp(π·i)=-1 perde le "esotericità" presunte).

e3) evitare di introdurre ("alla Dieudonné") un prodotto scalare predefinito (cosa che fra l'altro richiede la definizione di spazio vettoriale e, fatto di non ultimo momento, la precedente introduzione "asettica" dei numeri reali) e preparare la strada al prodotto vettoriale nello spazio tridimensionale riguardandolo come passaggio da ort, operatore lineare visto come prodotto vettoriale unario nel piano, ad un'operazione binaria (nello spazio tridimensionale), laddove non c'è un unico ortogonale "privilegiato" per un vettore, ma dove è possibile determinarne uno a partire da una coppia di vettori definendo così un'operazione (binaria) “bilineare”.

* * *

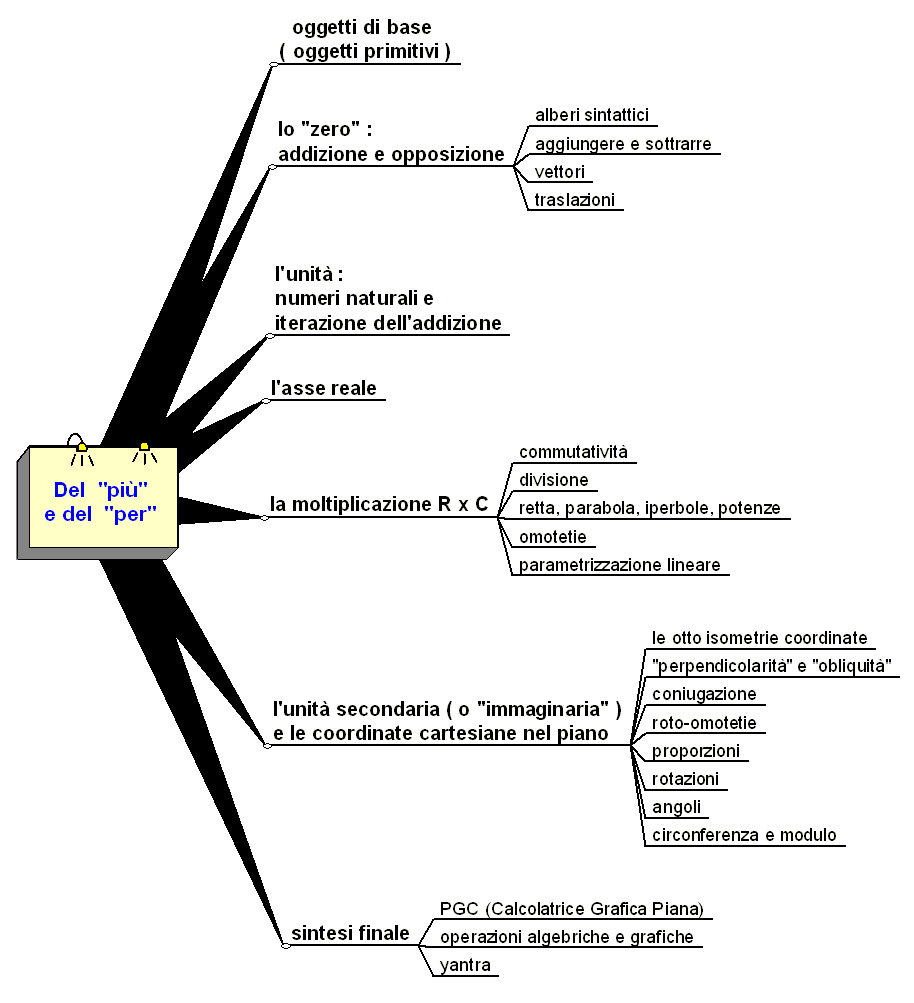
Mappa
(I link portano a pagine corredate di applet Java - visibili attualmente su pochissimi browser - prodotte nel 2008 nel quadro del Progetto EdA - Educazione degli Adulti - di INDIRE; il corrispondente materiale in Javascript, disponibile per ogni browser, è qui)