|

 
stiramento orizzontale di exp
- Sottoporremo adesso exp a delle trasformazioni dette stiramenti orizzontali, per ottenere da exp altre funzioni esponenziali
- chiamiamo stiramento orizzontale di rapporto s la trasformazione ( x , y )
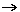 ( x•s , y ) (con s ≠ 0) ( x•s , y ) (con s ≠ 0)
- stiramento di exp:
f = exp = { (x,y) : y=exp(x) } 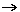 f' = { (x•s , y) : y=exp(x) } f' = { (x•s , y) : y=exp(x) }
f' = { (x',y): y=exp(x'/s) } = { (x,y): y=exp(x/s) }
- stiramento della retta tangente:
r = { (x,y) : y=x+1 } 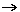 r' = { (x•s , y) : y=x+1 } r' = { (x•s , y) : y=x+1 }
r' = { (x',y): y=x'/s + 1 } = { (x,y): y=x/s + 1 }
- come f=exp è tangente a r in (0,1), così f' è tangente a r' in (0•s,1) = (0,1)
- prendendo k = 1/s, concludiamo che:
- la funzione esponenziale y=exp(kx) è tangente alla retta y=kx+1 nel punto (0,1)
- lim h → 0 ( 1 + k•h )1/h = base di f' = ek
- notiamo espressamente che la funzione f' , cioè y = exp(kx) = ekx = (ek)x, è l'esponenziale di base ek.
|

