determinazione dell'esponenziale passante per un dato punto P

• Preso un numero a reale positivo, la funzione x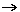a^x ha come grafico l'insieme dei punti (x,y) che verificano l'uguaglianza y=a^x.
  Tale funzione, come già sai, è detta esponenziale in base a e viene indicata con il simbolo   exp_a
   
• dal momento che per x=0 si ottiene a^x = a⁰ = 1, fra i vari punti del grafico della funzione esponenziale considerata c'è il punto ( 0 , 1 ). Prendendo invece x=1 si ottiene a^x = a¹ = a, per cui fra i vari punti del grafico della funzione esponenziale considerata c'è il punto ( 1 , a )
   
• pertanto, tutte le funzioni esponenziali passano per il punto ( 0 , 1 ) e per il punto di ascissa 1 e ordinata pari alla base.
  In formule:   (0,1) exp_a   e   (1,a) exp_a   per ogni a>0
   
• nella prima fase di questo percorso ci proponiamo di determinare quante e quali funzioni esponenziali passano, oltre che per il punto ( 0 , 1 ), anche per un dato punto P scelto a piacere e distinto da ( 0 , 1 ).