inversione di exp
e logaritmo naturale o neperiano

la pendenza della funzione esponenziale y=a^x nel punto (0,1) è la pendenza della retta r tangente, in tale punto, alla funzione esponenziale stessa
la retta r ha pendenza k tale che e^k = exp(k) = a

pertanto per determinare la pendenza in (0,1) di y=a^x bisogna determinare k dalla uguaglianza precedente, ossia invertire la funzione exp. Per far ciò:

definiamo la funzione inversa di exp:
ln := exp^-1 = { (x,y) : y=exp(x) }^-1 = { (y,x) : y=exp(x) } =
= { (x,y) : x=exp(y) }
(la funzione ln è detta logaritmo naturale o neperiano)
notiamo che y=exp(x) equivale a (x,y)exp, che equivale a (y,x)ln, che equivale ancora a x=ln(y). Pertanto da: e^k = exp(k) = a ricaviamo: k = ln(a)
rappresentiamo ln tenendo presente che la trasformazione (x,y)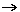(y,x) è la simmetria assiale rispetto alla bisettrice y=x (bisettrice del primo e del terzo quadrante).