le otto isometrie coordinate

• componendo coniugazione e inversione delle coordinate (che sono le due simmetrie di base), abbiamo visto come, in maniera piuttosto articolata, si perviene all'opposizione.
  Se componiamo invece in modo semplice, a due a due, l'opposizione, conj e inv otteniamo i seguenti operatori (tutti lineari, in quanto conj e inv lo sono):

• l' identit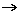à:   id: zz
• la coniugazione opposta:   - conj 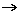: x+yi-x+yi
• la ortonormalità antioraria:   ort : x+y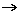i-y+xi
• la ortonormalità oraria:   - ort : x+y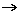iy-xi
• la inversione opposta:   - inv : x+yi-y-xi
   

• mettendo insieme queste 5 trasformazioni con le tre di partenza otteniamo 8 isometrie (trasformazioni che non modificano la forma e le dimensioni delle figure), che possono essere  suddivise  in:

• 4 simmetrie assiali:   conj, -conj, inv, -inv
• 4 rotazioni:   id, ort, -id (l'opposizione), -ort

• possiamo esprimere tutte le 8 isometrie coordinate tramite una simmetria assiale (conj) e una delle due ortonormalità, ad esempio l'antioraria ort. Pertanto la simmetria assiale conj e la rotazione ort costituiscono due isometrie di base.