|


unità immaginaria e numeri complessi
- ortonormalità di 1 e i: introduciamo graficamente il punto i come quel punto che dista da 0 quanto ne dista 1 e che sta a sinistra di 0 guardando 1.Tale configurazione grafica è detta ortonormale.
Matematicamente, invece, richiederemo solo il seguente:
- assioma dell'unità immaginaria:
i non è in R
- la retta I := R•i è detta asse immaginario. Graficamente tale asse è perpendicolare all'asse reale R. C è generato dai punti 1 e i mediante l'addizione (che è basata sul punto 0) e la moltiplicazione lineare, ossia C è generato dalle combinazioni lineari di 1 e i. In tal senso si può asserire che i punti 0, 1, i sono i punti basilari su cui poggia C (per tre punti passa uno ed un solo piano). Considerando 1, i e gli altri punti di C come vettori (quindi riferiti all'origine 0), ogni altro vettore di C è esprimibile come combinazione lineare di 1 e i, ossia a partire da una coppia di vettori indipendenti (infatti i non appartiene a R). E' questo il contenuto dell'ultimo assioma della teoria:
- assioma di bidimensionalità:
C = R + I
Per cui si ha: C = R + R•i = { x + y•i : x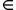 R, y R, y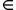 R}. R}.
I numeri reali x e y sono detti coordinate del
numero complesso x+y•i
(con la notazione breve per la moltiplicazione: x+yi)
- espressione dell'opposto tramite coniugazione e inversione delle coordinate:
- z = inv( conj( inv( conj(z) ) ) ) = ( ( (z-)*)-)* = z - * - *
|

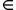 R, y
R, y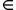 R}.
R}.

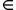 R, y
R, y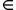 R}.
R}.