|


le isometrie dirette (o movimenti)
- rotazione seguita da traslazione (roto-traslazione): è una trasformazione composta del tipo
Tv
 Ru con u Ru con u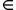 U e v U e v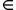 C C
- una figura F viene trasformata da una roto-traslazione in una figura F' che non solo mantiene sia la forma sia la grandezza di F, ma è ottenibile a partire da F senza uscire dal piano C, ossia con un movimento, "dentro" al piano stesso, che sovrappone F a F'.
Per contro, la coniugazione porta una figura in un'altra di uguale forma e grandezza, ma ottenibile da quella di partenza solo con un ribaltamento intorno all'asse reale, quindi "uscendo" dal piano.
Le roto-traslazioni sono perciò dette isometrie dirette o movimenti
- formula di un'isometria diretta: ricaviamo subito, dalla definizione:
(Tv
 Ru)(z) = u•z + v Ru)(z) = u•z + v
- traslazione seguita da rotazione: anche
Ru
 Tv è una roto-traslazione, in quanto: Tv è una roto-traslazione, in quanto:
(Ru Tv)(z) = u(z+v) = uz+uv = (Tu v Tv)(z) = u(z+v) = uz+uv = (Tu v Ru)(z), Ru)(z),
per cui: Ru Tv = Tu v Tv = Tu v Ru Ru
- proprietà dei movimenti:
- la composizione di movimenti dà un movimento: infatti, tenendo presente l'associatività della composizione di funzioni, nonché il criterio appena illustrato per scambiare l'ordine di composizione di rotazione e traslazione, si ha:
(Tv' Ru') Ru') (Tv (Tv Ru) =
Tv' Ru) =
Tv' (Ru' (Ru' Tv) Tv) Ru =
Tv' Ru =
Tv' (Tu'v (Tu'v Ru') Ru') Ru =
(Tv' Ru =
(Tv' Tu'v) Tu'v) (Ru' (Ru' Ru) = Tv'+u'v Ru) = Tv'+u'v Ru'u Ru'u
- l'identità come movimento nullo: osserviamo che id = T0 = R1 = T0
 R1 R1
- inversione di un movimento: il movimento
Tv
 Ru composto con il movimento R1/u Ru composto con il movimento R1/u T-v dà l'identità T-v dà l'identità
- preservazione dell'orientamento:
dati tre punti A, B, C e un movimento che li porti rispettivamente in A', B', C', i percorsi ABC e A'B'C' sono o entrambi orari o entrambi antiorari (brevemente si dice che sono concordi).
|

