|
l o g a r i t m i : proprietà ( regole di calcolo ) fondamentali |
|
|
Partiamo da: y = ax ( a > 0 ) |
|
|
y = expa ( x ) ( definizione di exp ) |
x = loga ( y ) ( definizione di log ) |
|
y' = expa ( x' ) |
x' = loga ( y' ) |
| y · y' = expa ( x ) · expa ( x' ) | x + x' = loga ( y ) + loga ( y' ) |
|
a x + x' = a x · a x' ( proprietà della somma degli esponenti ) |
|
|
y · y' = ax · ax' = ax+x' = expa ( x + x' ) |
=> x + x' = loga ( y · y' ) |
| expa ( x + x' ) = expa ( x ) · expa ( x' ) | loga ( y ) + loga ( y' ) = loga ( y · y' ) |
|
(1) regola del logaritmo di un prodotto : loga ( y · y' ) = loga ( y ) + loga ( y' ) |
|
|
a x x' = ( a x ) x' ( proprietà del prodotto degli esponenti ) |
|
|
y = expa ( x ) |
x = loga ( y ) |
|
yc = ( expa(x) )c = ( ax )c = ax·c = expa(x·c) |
=> x c = loga ( y c ) |
| expa ( x · c ) = ( expa (x) ) c | loga (y) · c = loga ( y c ) |
| (2) regola del logaritmo di una potenza : loga ( y c ) = c · loga (y) | |
| c = -1 | b = y c ( => c = logy (b) ) |
| loga ( y -1 ) = (-1) · loga (y) | loga (y c) = loga (y) · c = loga (y) · logy (b) |
| loga ( 1 / y ) = - loga ( y ) | loga ( b ) = loga (y) · logy (b) |
|
loga( z / y )=loga(z · 1/y)=loga(z) - loga(y) |
logy ( b ) = loga ( b ) / loga ( y ) |
| ^ regola del logaritmo di un quoziente | ^ regola del cambiamento di base |
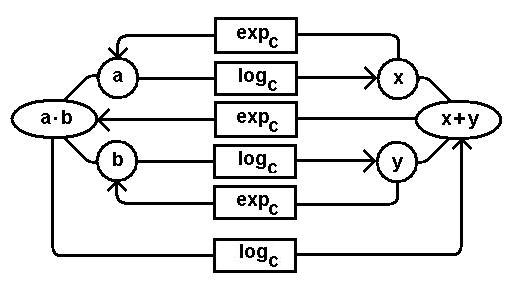
i morfismi esponenziale e logaritmico
| x | → | expa | → | u | ||
| ← | loga | ← | ||||
| + | x + y | → | expa | → | u · v | · |
| ← | loga | ← | ||||
| y | → | expa | → | v | ||
| ← | loga | ← | ||||
| expa(x+y)=ax+y=ax·ay=expa(x)·expa(y)=u·v |
| loga(u·v) = loga(u) + loga(v) = x + y |
|
Logaritmo di potenza (logaritmo di esponenziale) : loga bx = x · loga b |
|
|
|
Quando b=a
(porta col mouse b a coincidere con a)
|
|
cambiamento di base nei
logaritmi : logb x = ( loga x ) / ( loga
b ) ( da: loga x = loga b(logbx) = logb x · loga b = loga b · logb x ) |
| Nella figura sono
rappresentate expa ,
expb , loga
, logb ; k è quel numero tale che ak=b , quindi k=logab ; la figura illustra che bx = akx e che quindi, per simmetria rispetto a y=x, logax = k·logbx ( ovvero: logax = logab · logbx ) |